To solve the problem we will assume the following:
1. Air behaves as an ideal gas during all the process.
2. The initial air equivalent to 8200L is at atmospheric pressure. It means 1 atm.
3. The temperature remains constant.
Taking into account the above, we can apply the Boyle-Marriote Law that relates the change in pressure and volume at constant temperature. The equation that we will use will be:
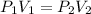
Where,
P1 is the atmospheric pressure. 1atm
V1 is the initial volume of air required, 8200L
P2 is the final pressure we want to find
V2 is the final volume, it means the volume of the spherical air tank. We will calculate this volume using the volume equation for a sphere:
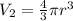
r is the radius of the sphere, r=73cm/2=36.5cm
So, the volume of the spherical air tank will be:
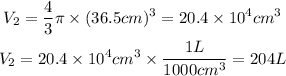
No, we clear P2 from the first equation and replace known data:

The pressure of the gas must be 40.3 atm
Answer: 40.3