1 Answer

LiveRock · Answer 1 · 2023-02-10T00:58:05+0000

The equation of a circle is given by:

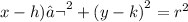
$\lparen x-h)\placeholder{⬚}^2+\left(y-k\right)^2=r^2$

where (h,k) is the center and r is the radius.

In this case we know that the center of the circle is (-4,3). To find the radius we just need to remember that the radius is half the diameter, hence:

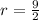
Plugging the values for the center and the radius we have that:

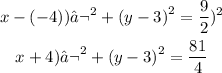
$\begin{gathered} \lparen x-\left(-4\right))\placeholder{⬚}^2+\left(y-3\right)^2=\lparen(9)/(2))^2 \\ \lparen x+4)\placeholder{⬚}^2+\left(y-3\right)^2=(81)/(4) \end{gathered}$

Therefore, the equation of the circle is:

$\operatorname{\lparen}x+4)\placeholder{⬚}^2+\left(y-3\right)^2=(81)/(4)$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions