Given the following question:
Filling a table of values is very simple when we are already given the values of x, so what we need to do to fill in the rest of the table for f(x) and g(x) is substitute x for each of the table values given for x.
To start off we are given 1 so we substitute 1 in for x in both f(x) and g(x) and solve.
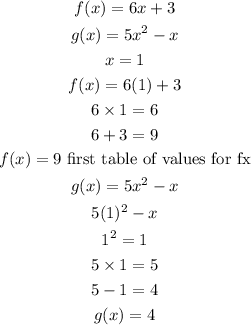
Second table of values:
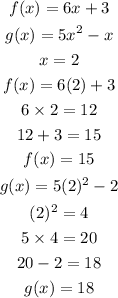
Third table of values:
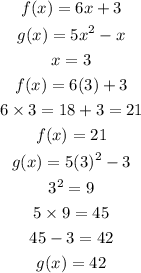
Final table of values:
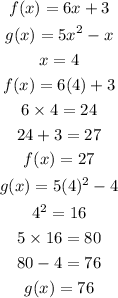
g(x)=5x^2-x eventually exceeds f(x) given the table of values.