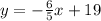Question

Write the equation in slope-intercept form for the line that passes through the given pointand is perpendicular to the given equation.5 x– 6 y= 18and passes through (10,7)

Answer 1

The equation of a line is given by

`y-y_1=m(x-x_1)`

To find this equation we need the slope and a point where the line passes through.

In our case we know the point but we don't know the slope yet.

To Find the slope we have to use the fact that the line is perpendicular to

`5x-6y=18`

First, we have to remember that two lines are perpendicular if and only if

`m_1m_2=-1`

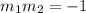
The slope of the line 5x-6y=18 is 5/6. Plugging this value in the equation above and solving it for m1 we have:

`\begin{gathered} m_1((5)/(6))=-1 \\ m_1=-(1)/((5)/(6)) \\ m_1=-(6)/(5) \end{gathered}`

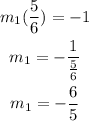
Once we have the slope and the point we can find the equation of the line, in our case we have

`\begin{gathered} y-7=-(6)/(5)(x-10) \\ y-7=-(6)/(5)x+12 \\ y=-(6)/(5)x+19 \end{gathered}`

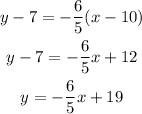
Therefore the line we are looking for is

`y=-(6)/(5)x+19`