Part (i)
Free body diagram of the 1.5 kg block;
Part (ii)
Only 1 force is acting on the pulley is the weight of the block attached with the sting. The torque acting on the pulley is given as,
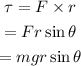
Here, g is the acceleration due to gravity and the θ is the angle between force F and r (as force is acting tangentially hence θ=90°)
Substituting all known values,
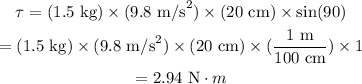
In rotational dynamics torque is given as,
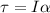
Here, I is the moment of inertia of the pulley (I=2 kg.m²) and α is the angular acceleration.
The angular acceleration is given as,
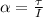
Substituting all known values,
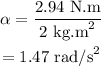
The angular velocity is given as,
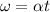
Here, t is the time.
Substituting all known values,
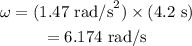
Therefore, the angular velocity of the pulley is 6.174 rad/s.
The angular displacement of the pulley in 4.2 s is given as,
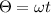
Substituting all known values,
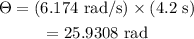
The number of revolutions of the