If the roots of the quadratic equation are -2 and -5, then the factors of the quadratic equation must be:
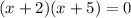
The quadratic equation in standard form goes by this pattern:

So, to be able to find the standard form of the quadratic equation, let's multiply the two factors:
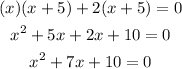
Therefore, the quadratic equation in standard form of the given roots is x² + 7x + 10 = 0.