Answer:
• x-intercept: (-1.5, 0).
,
• y-intercept: (0, 1).
Explanation:
Given the function:
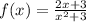
(a)x-intercept
The x-intercept is the value of x at which f(x)=0.
When f(x)=0

The x-intercept is located at (-1.5, 0).
(b)y-intercept
The y-intercept is the value of f(x) at which x=0.
When x=0
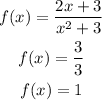
The y-intercept is at (0, 1).
(c)Graph
The graph of f(x) is given below: