Question

24 / sq root of x-16 - sq root of x = sq root of x-16

Answer 1

The given equation is

`(24)/(√(x-16))-√(x)=√(x-16)`

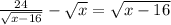
First, we multiply both sides to the square root of (x-16), as follows

`\begin{gathered} ((24)/(√(x-16))-√(x))\cdot√(x-16)=√(x-16)\cdot√(x-16) \\ (24\cdot√(x-16))/(√(x-16))-√(x)\cdot√(x-16)=x-16 \\ 24-√(x(x-16))=x-16 \end{gathered}`

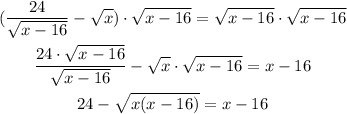
Now that we have just one root, we can subtract 24 on both sides

`\begin{gathered} 24-√(x(x-16))-24=x-16-24 \\ -√(x(x-16))=x-40 \end{gathered}`

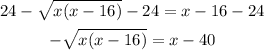
Then, we elevate both sides to the square power

`\begin{gathered} (-√(x(x-16)))^2=(x-40)^2 \\ x(x-16)=x^2-2(40)x+40^2 \\ x(x-16)=x^2-80x+1600 \end{gathered}`

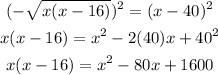
To solve (x-40)2, we used the formula

`(a-b)^2=a^2-2ab+b^2`

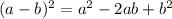
Now, we solve for x

`\begin{gathered} x^2-16x=x^2-80x+1600 \\ x^2-x^2-16x+80x=1600 \\ 64x=1600 \end{gathered}`

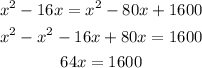
At last, we divide the equation by 64

`\begin{gathered} (64x)/(64)=(1600)/(64) \\ x=25 \end{gathered}`

Therefore, the solution is 25.