Question

Solve and graph the following system. Please use my graph to plot the points. 3x-2y=182x+4y=-4

Answer 1

We have to solve and graph the following system of equations:

`\begin{gathered} 3x-2y=18 \\ 2x+4y=-4 \end{gathered}`

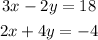
We can solve this graphically: the solution will be the intersection of both lines, as this is the only point that satisfy the two equations.

We start by graphing the first equation.

We have it expressed in standard form, so we can find the x-intercept and y-intercept.

The x-intercept (y = 0) will be:

`\begin{gathered} 3x-2(0)=18 \\ 3x=18 \\ x=(18)/(3) \\ x=6 \end{gathered}`

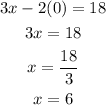
Then, the x-intercept is (6,0).

The y-intercept (x = 0) will be:

`\begin{gathered} 3(0)-2y=18 \\ -2y=18 \\ y=(18)/(-2) \\ y=-9 \end{gathered}`

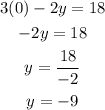
Then, the y-intercept is (0,-9).

With two points we can graph the line as:

We can repeat the process for the second line.

First we simplify it:

`\begin{gathered} (2x+4y)/(2)=(-4)/(2) \\ x+2y=-2 \end{gathered}`

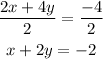
Then, we can find the x-intercept (y = 0) as:

`\begin{gathered} x+2(0)=-2 \\ x=-2 \end{gathered}`

The y-intercept (x = 0) will be:

`\begin{gathered} (0)+2y=-2 \\ y=-(2)/(2) \\ y=-1 \end{gathered}`

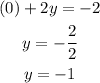
Then, we have the two intercepts: (-2, 0) and (0, -1).

We can graph this line as:

The lines intersect at (4,-3) which is the solution to the system.