Let the function
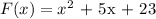
The quadratic formula is:
So, the zeros of the function F(x)=x^2+5x+23 are the solutions x´s for the equation:
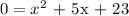
these solutions can be found using the quadratic formula.
Then, we will use the quadratic formula with a = 1, b = 5, and c = 23. That is:
that is equivalent to say:
![\frac{-5\text{ +/- }\sqrt[]{25\text{ - 92}}}{2}\text{ = }\frac{-5\text{ +/- }\sqrt[]{-67}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/8ai2fkhem1sm44npt5hzck5khu15qgef73.png)
but
![\sqrt[]{-67\text{ }}=\text{ }i\text{ }\sqrt[]{67}](https://img.qammunity.org/2023/formulas/mathematics/college/vr7npcrmvdlhvag1ih46z7nqvr2ywfu2to.png)
so, we have
![\frac{-5\text{ +/- }\sqrt[]{25\text{ - 92}}}{2}\text{ = }\frac{-5\text{ +/- }\sqrt[]{-67}}{2}\text{ = }\frac{-5\text{ +/- }\sqrt[]{67}i}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/yrbzyl6haj66s0p1nq6o9s2wgyvk4t5fxm.png)
We can conclude that the zeros for F(x)=x^2+5x+23 are
![\text{ }\frac{-5\text{ + }\sqrt[]{67}i}{2}\text{ and }\frac{-5\text{ - }\sqrt[]{67}i}{2}\text{ , those zeros are imaginary numbers.}](https://img.qammunity.org/2023/formulas/mathematics/college/vi4rsyyohs8tutycgoa1asfydk002aaz3j.png)