We can draw the circuit and the position of the car in order to help us understand the problem:
We can calculate how many radians represent this arc by calculating some proportions.
We know that x is to 2*pi (the complete lap) radians as 56 meters is to the circumference of the race track.
As the circumference of the racetrack is 2*pi*r, we can write:
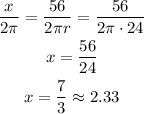
How many radians has the racecar swept out?
2.33 radians
If we draw a vertical axis that goes through the center of the race track, we can calculate the distance from the car to that axis as:
the distance to the vertical axis is equal to the projection of the radius on the horizontal axis. This projection has the value of the radius multiplied by the cosine of the angle x.
We then can calculate the distance to the vertical axis as:
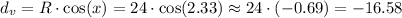
The race car is in the second quadrant and the distance to the vertical axis is 16.58 meters from the left of the center of the race track.
What is the racecar's distance to the right of the center of the race track (in meters)?
16.58 meters.
We know have to calculate the distance to the horizontal axis.
This distance is the projection of the radius into the vertical axis, so it can be calculated as:
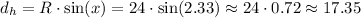
What is the racecar's distance above the center of the race track (in meters)?
17.35 meters.
If d is the distance to the vertical axis, it can be expressed in function of the angle x as:
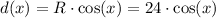
The expression to represent the racecar's distance to the right of the center of the race track is d(x)=24*cos(x).
If we want the expression for the distance to the horizontal axis, we can write:
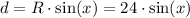
The expression to represent the racecar's distance above the center of the race track is d(x)=24*sin(x).
Answer:
What is the racecar's distance to the right of the center of the race track (in meters)?
16.58 meters.
What is the racecar's distance to the right of the center of the race track (in meters)?
16.58 meters.
What is the racecar's distance above the center of the race track (in meters)?
17.35 meters.
The expression to represent the racecar's distance to the right of the center of the race track is d(x)=24*cos(x).
The expression to represent the racecar's distance above the center of the race track is d(x)=24*sin(x).