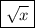1 Answer

Jme · Answer 1 · 2023-04-29T13:54:19+0000

We want to simplify the expression

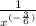
$\frac{1}{x^{(-(3)/(6))}}$

First we will simplify the exponent:

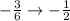
$-(3)/(6)\rightarrow-(1)/(2)$

So now we have

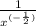
$\frac{1}{x^{(-(1)/(2))}}$

Next, we need to apply the negative exponent property, which states that for any positive value of m and n,

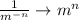
$(1)/(m^(-n))\rightarrow m^n$

(We flip the fraction to the its reciprocal, then change the sign of the exponent.)

Our new expression is:

$x^{(1)/(2)}$

Finally, we need to apply the rational exponent rule. Which states for any positive integer value of m and n,

$x^{(m)/(n)}=\sqrt[n]{x^m}$

Notice the n becomes the index of the radical, and the m becomes the power of the number under the radical.

So, we have

$\sqrt[2]{x}^1\rightarrow√(x)$

Our final answer is

$\boxed{√(x)}$

Please log in or register to add a comment.