Question

Find the values of x and y that make the triangles similar.

Answer 1

Given the similar triangles

The proportion/ratio of the similar triangles are

`(12)/(16)=(6)/(x)=(8)/(y)`

To find the values of x and y, take into consideration the given propotion i.e

`\begin{gathered} (12)/(16)=(6)/(x) \\ \text{Crossmultiply} \\ 12x=96 \\ \text{Divide both sides by 12} \\ (12x)/(12)=(96)/(12) \\ x=8 \end{gathered}`

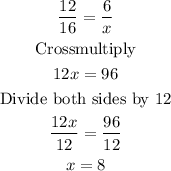
Hence, the value of x is 8.

For the value of y

`\begin{gathered} (12)/(16)=(8)/(y) \\ \text{Crossmultiply} \\ 12y=128 \\ \text{Divide both sides by 12} \\ (12y)/(12)=(128)/(12) \\ y=(32)/(3) \end{gathered}`

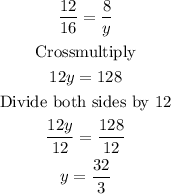
Hence, the value of y is 32/3

Thus the value of x = 8 and y = 32/3