Let be "f" the hotel charge (in dollars) in the first city before tax and "s" the hotel charge (in dollars) in the second city before tax.
According to the information given in the exercise, the hotel charge before tax in the second city was $1500 lower than in the first city. Then, you can set up the following equation to represent this situation:
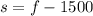
And, knowing the taxes in each city and the total hotel tax paid for both cities, you can set up the second equation:
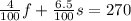
Remember that you can write a percent in decimal form by dividing it by 100.
Then, the System of Equations is:
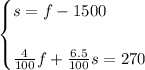
In order to solve it, you can use the Substitution Method:
1. Substitute the first equation into the second equation:
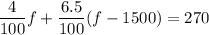
2. Solve for "f":
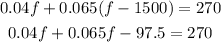
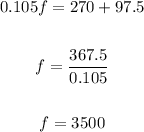
3. Substitute the value of "f" into the first equation:
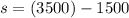
4. Evaluating, you get:
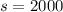
Therefore, the answer is:
- First city: $3,500
- Second city: $2,000