Given:
Fuel efficiency of the first car = 20miles/gallon of gas
Fuel efficiency of the second car = 35 miles/gallon of gas
Total miles covered on a particular week = 925 miles
Total gas consumed = 35 gallons
Solution
Let the gallons of gas consumed by the first car is x, and the gallons of gas consumed by the second car be y.
From the last information, we have:
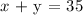
The distance covered by the first car in the said week is:
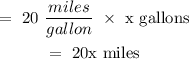
The distance covered by the second car in the said week is:
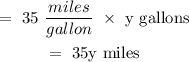
From the third statement, we have:
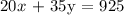
To obtain x and y, we can solve the equations simultaneously
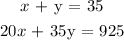
Solving simultaneously, we have:
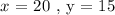
Answer:
First car: 20 gallons
Second car: 15 gallons