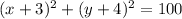Question

Find the center and the radius of the circle and please show all of your work and the equation of the circle in center radius form. x ^ 2 + y ^ 2 + 6x + 8y - 75 = 0

Answer 1

Given:

`x^2+y^2+6x+8y-75=0`

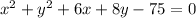
To find the circle equation in center and radius form:

Let us rewrite the equation as

`\begin{gathered} x^2+y^2+6x+8y-75=0 \\ x^2+6x+y^2+8y-75=0 \\ (x^2+6x+3^2)-3^2+(y^2+8y+4^2)-4^2-75=0 \\ (x+3)^2-9+(y+4)^2-16-75=0 \\ (x+3)^2-9+(y+4)^2-16-75=0 \\ (x+3)^2+(y+4)^2-100=0 \\ (x+3)^2+(y+4)^2=100 \end{gathered}`

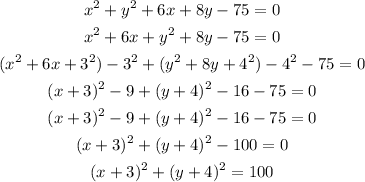
Thus, the equation of the circle in center-radius form is,

`(x+3)^2+(y+4)^2=100`

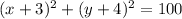
The general equation of the circle in center-radius form is,

`(x-h)^2_{}+(y-k)^2=r^2`

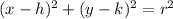
Where (h, k) is the center and r is the radius.

So, comparing we get

The center is,

`(-3,-4)`

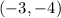
The radius is,

`r=10`

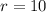
The equation of the circle in center-radius form is,

`(x+3)^2+(y+4)^2=100`