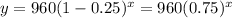The exponential decay formula is:
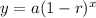
where y and x are the variables, a is the initial value, and r is the decay rate (as a decimal)
In the case of the values of a computer, the initial value is 960, that is, a = 960. y represents the value of the computer and x represents time. Substituting with x = 1, y = 720, and a = 960, we wet:
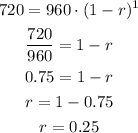
Now we can check if this model predicts correctly the other values of the table.
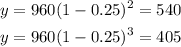
These results show that the value of the computer decay by a constant percentage rate per year.
The equation is: