INFORMATION:
We know that:
- A rain drop hitting a lake makes a circular ripple
- the radius, in inches, grows as a function of time in minutes according to r(t) = 25√(t+2)
And we must find the area of the ripple as a function of time and the area of the ripple at t=2
STEP BY STEP EXPLANATION:
To find it, we must:
1. Write the equation for the area of a circle

2. Write the given equation for the radius
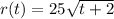
3. Replace the equation for the radius in the equation for the area of a circle
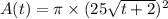
4. Find the area when t = 2 replacing it in the function for the area
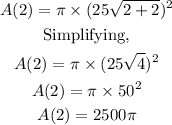
Finally, the area of the ripple at t=2 is 2500π in^2
ANSWER:
Area of the ripple as a function of time:
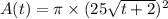
Area of the ripple at t=2:
A = 2500πin ^2