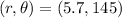We are asked to write each of the following vectors in the polar form ⟨r,θ⟩
Where r is the vector's magnitude (in miles) and θ is the vector's angle (in degrees) swept .
1) 12 miles in the direction 45° north of east:
Let us draw a figure to better understand the problem
As you can see, the magnitude is 12 and the angle is 45° measured counter-clockwise from the due east direction.
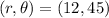
2) 1.59 miles in the direction 10° west of south:
Let us draw a figure to better understand the problem
As you can see, the magnitude is 1.59 and the angle is 190° measured counter-clockwise from the due east direction.
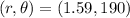
3) 5.7 miles in the direction opposite of 35° south of east:
Let us draw a figure to better understand the problem
Please note that opposite of 35° south of east is west of north.
As you can see, the magnitude is 5.7 and the angle is 145° measured counter-clockwise from the due east direction.