The exponential model for decay/decline is given by the formula:
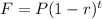
Where
P is the present value
r is the rate of decline per time period
t is the time period
F is the future value
Given,
initial population is 11 million (P = 11)
declining rate of 2.6% [in decimal, 2.6/100 = 0.026, r = 0.026]
time is 15 years [t = 15]
Substituting the given values into the formula, let's find "F", population after 15 years:
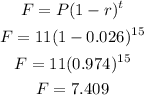
Rounded to 2 decimal place, the population after 15 years would approximately be equal to
7.41 million