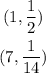Answer:
(1, 1/2) and (7, 1/14)
Explanation:
Given:
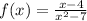
The point(s) at which the graph of the function has a horizontal tangent line is the point at which the first derivative is zero.
First, find the first derivative of f(x) using the quotient rule.
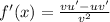
From f(x):
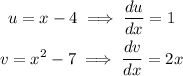
Substitute into the quotient rule:
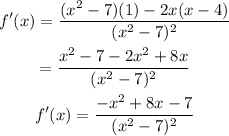
Set the derivative equal to 0:
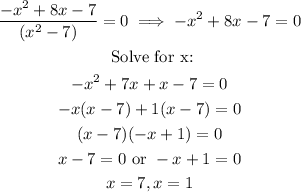
Finally, find the corresponding values of f(x).
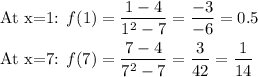
The points at which the graph of the function has a horizontal tangent line are: