Question

Find the equation of the line which passes through M(2.5) and which is parallel to the line which passes through A (2.5) and B (4.13)

Answer 1

Gie\ven that the line which passes through A (2.5) and B (4.13)​ is parallel to the line which passes through the point M(2,5).

Consider points A (2.5) and B (4.13)​.

Recall the formula for the slope is

`m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)`
`\text{ Substitute }* x_1=2,x_2=4,y_1=5\text{ and }y_2=13,\text{ we get}`

`m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)=(13-5)/(4-2)=(8)/(2)=4`

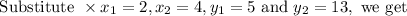
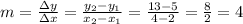
We get the slope m=4.

We know the parallel lines have an equal slope.

The general form of the required line equation is

`y=mx+b`

Substitute m=4, we get

`y=4x+b`

This line is passing through point M(2,5).

Substitute x=2 and y=5 in y=4x+b, to find the value of b.

`5=4(2)+b`

`5=8+b`

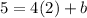
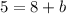
Subtracting 8 from both sides, we get

`5-8=8+b-8`

`-3=b`

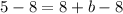
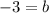
We get b=-3.

Substitute b=-3 in y=4x+b, we get

`y=4x-3`

Hence the required line equation is y=4x-3.