Question

If the value of a car over time can be modeled by theequation y = 21000(0.88)*, which of the followingequations are true?

Answer 1

the car was bought for $21,000, and is losing 12% of its value each year (option C)

Step-by-step explanation:

The given model:

`y=21000(0.88)^x`

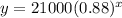
The value in the bracket is less than 1. So, it exponential decay

For exponential decay:

`\begin{gathered} y=a(1-r)^x \\ \text{where a = initial amount} \\ r\text{ = rate} \\ x\text{ = time } \end{gathered}`

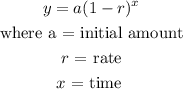
comparing both equations:

`\begin{gathered} y\text{ = y} \\ a\text{ = 21,000, }x\text{ = x} \\ 0.88\text{ = 1-r} \\ \text{subtract 1 fromboth sides:} \\ 0.88\text{ - 1 = 1-r - 1} \\ -0.12\text{ = -r} \\ \text{divide both sides by -1:} \\ -\frac{0.12}{-1\text{ }}=\frac{\text{ -r}}{-1} \\ r\text{ = 0.12} \\ \\ \end{gathered}`

r = 12%

The dcay means a deduction in original amount

Hence, the car was bought for $21,000, and is losing 12% of its value each year (option C)