Question

Colin is making a 10-1b bag of trail mix for his upcoming backpacking trip. Ifchocolates cost $3.00 per pound and mixed nuts cost $6.00 per pound and Colin hasa budget of $5.40 per pound of trail mix, how many pounds of each should he use?

Answer 1

We first create a system of equations that can represent the problem given.

We let x represent the amount of chocolates, in pounds, and y be the amount of mixed nuts, also in pounds. Colin has a total of 10-lb bag of trail mix. We can write an equation representing this as:

`x+y=10`

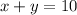
Chocolate costs $3.00 per pound while mixed nuts cost $6.00 per pound. Colin's total budget is around $5.40 per pound. This can be represented in equation as:

`\begin{gathered} 3x+6y=10(5.40) \\ 3x+6y=54 \end{gathered}`

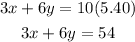
Hence, we now have the system of equations written as:

`\begin{gathered} x+y=10 \\ 3x+6y=54 \end{gathered}`

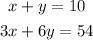
Solve the system of equations using methods of elimination, as follows:

`\begin{gathered} -3(x+y=10) \\ 3x+6y=54 \\ \\ -3x-3y=-30 \\ 3x+6y=54 \\ \\ 3y=24 \\ y=8 \end{gathered}`
`\begin{gathered} x+8=10 \\ x=10-8 \\ x=2 \end{gathered}`

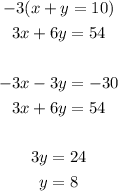
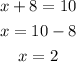
Therefore, Colin used 2 pounds of chocolates and 8 pounds of mixed nuts for this 10-lb trail mix.