Solution:
Given:
Population of the world in 1987 = 5 billion
Annual growth rate = 1.2% per year.
We want to determine the projected world population in 2019.
An exponential growth can be modelled by the function
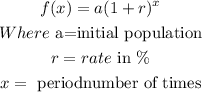
For the question before us,
r=1.2% = 0.012
x = 2019 -1987 = 32
a = 5,000,000,000
Thus,

The projected world population in 2019 is 7,323,967,432.5