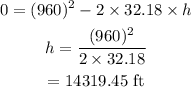Given:
The initial velocity of the pumpkin is

To find the maximum height of the pumpkin
and the time for which pumpkin will be air.
Step-by-step explanation:
When the pumpkin reaches maximum height its final velocity will be
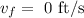
The equation used to calculate the maximum height will be
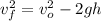
Here, the value of g is the acceleration due to gravity whose value is 32.18 ft/s^2.
On substituting the values, the maximum height will be