Solution
(A). We are given a 1 x 1 x 3 solid.
(B). If it is enlarged by a scale factor of 2, The new dimension will be 2 x 2 x 6
(C). Here we will find the surface Area of the New divided by the surface area of the former
The number (n) needed is

Therefore, four 1 x 1 x 3 solids would be needed
(D).
Scale factor = 3
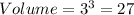
The volume would be 27 times larger