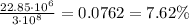The voltage generates a force over the electron, this force is the one we use to calculate the acceleration
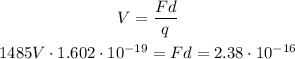
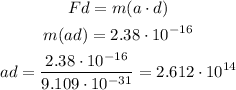
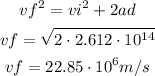
First, we apply the energy equation to find the Fd result based on voltage. Then we find the acceleration times distance. Finally, we find the speed with a kinematic equation.
Now I'm going to find the percentage of the speed of light.