Question

I need help, I am struggling with this Look at the top of the picture to see the instructions this is from my trigonometry prep guide.

Answer 1

For the given angles, we will find the quadrant that angle lies in it.

Before we begin, the limits of each quadrant is as follows:

Quadrant I: 0 < θ < π/2

Quadrant II: π/2 < θ < π

Quadrant III: π < θ < 3π/2

Quadrant IV: 3π/2 < θ < 2π

Now, we will check the angles:

The first angle: 3π/4

The angle lies between π/2 and π

So, it is in Q II

===================================

The second angle: 57π/8

We will subtract the multiple of 2π to get the standard angle

`(57\pi)/(8)=(57\pi)/(8)-3\cdot2\pi=(9\pi)/(8)`

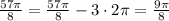
The angle 9π/8 lies between π and 3π/2

So, the angle lies in Q III

===================================

The third angle 13π/6

`(13\pi)/(6)=(13\pi)/(6)-2\pi=(\pi)/(6)`

The angle π/6 lies between 0 and π/2

So, the angle lies in Q I

=====================================

The fourth angle (-35π/4)

We will add (2π) or a multiple of (2π) to find the positive standard angle

`-(35\pi)/(4)=-(35\pi)/(4)+5\cdot2\pi=(5\pi)/(4)`

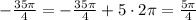
the angle 5π/4 lies between π and 3π/2

So, the angle lies in Q III

=========================================

The fifth angle (-5π/6)

`-(5\pi)/(6)=-(5\pi)/(6)+2\pi=(7\pi)/(6)`

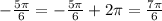
The angle 7π/6 lies between π and 3π/2

So, the angle lies in Q III

==========================================

The last angle (-5π/11)

`-(5\pi)/(11)=-(5\pi)/(11)+2\pi=(17\pi)/(11)`

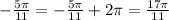
The angle 17π/11 lies between 3π/2 and 2π

So, the angle lies in Q IV

===================================================

So, the answer will be as shown in the following picture: