Question

The graph of Fx), shown below, has the same shape as the graph of G(x) = x4, but it is shifted to the right 1 unit. What is its equation? -6 5

Answer 1

When a function f(x) is equal to another function g(x) but shifted one unit to the right, we can compare points of equal value for f(x) and g(x) to relate the equations.

For example, f(x) has its vertex at x = 1 and g(x) has its vertex at x = 0.

As they represent the same point for the function, we can write:

`g(0)=f(1)`

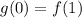
We can generalize this for any point as:

`g(x)=f(x+1)`

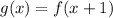
Also, we can write:

`g(x-1)=f(x-1+1)=f(x)`

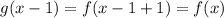
Then, we now know that f(x) is equal to g(x-1) for any value of x.

Knowing the equation of g(x), we can find f(x) as:

`\begin{gathered} f(x)=g(x-1) \\ f(x)=(x-1)^4 \end{gathered}`

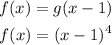
Answer: f(x) = (x-1)^4 [Option D]