Solution
From the given graph
The standard form of a rational function is
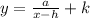
The zero(s) of the graph is at x = 2, the factored form is
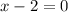
The y-intercept of the given function is at y(0) = 1
The vertical asymptote is at x = -3 (odd function) and x = 4 (even function)
The factored form is

The rational function becomes,
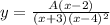
Where x = 0 and y(0) = 1
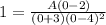
Solve for A
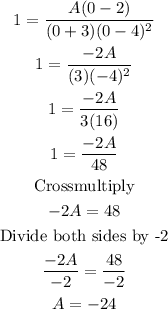
The rational function is

Hence, the numerator is
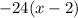
Hence, the denominator is
