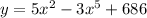Question

The derivative of function y is dy/dx = 10x - 12x³. Determine particular solution if initial condition is y(3) - 2.

Answer 1

The problem requires the solution of a differential equation. The first step in this case is let "dy" alone as follows:

`dy=(10x-12x^3)dx`

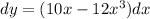
Now we have to integrate each part of the equality.

`\int dy=\int(10x-12x^3)dx`

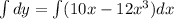
The left side is the integral of "1":

`\int dy=y+c`

Where "c" is a unknown constant. Now the right side as follows:

`\int(10x-12x^3)dx=5x^2-3x^5`

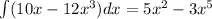
Where we did not add another constant becase we already did it on the left side of the equation. Now:

`\begin{gathered} y+c=5x^2-3x^5 \\ y=5x^2-3x^5-c \end{gathered}`

Finally, we consider the initial condition y(3)=2 to find the value of "c" as follow:

`\begin{gathered} y(3)=5(3)^2-3(3)^5-c=2 \\ 5(3)^2-3(3)^5-2=c \\ c=-686 \\ \end{gathered}`

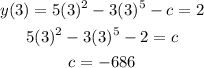
Hence, the particular solution is:

`y=5x^2-3x^5+686`