Question

Find the desired slopes and lengths then fill in the words that characterize the triangle

Answer 1

The points on the plane that define the triangle are

`Q=(6,-8),R=(1,-5),S=(4,0)`

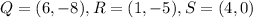
Those three points define three segments whose slopes are given by the formula.

`m=(y_2-y_1)/(x_2-x_1)`

Therefore,

`\begin{gathered} m_(QR)=(-8-(-5))/(6-1)=-(3)/(5) \\ m_(RS)=(-5-0)/(1-4)=-(5)/(-3)=(5)/(3) \\ m_(SQ)=(-8-0)/(6-4)=-(8)/(2)=-4 \end{gathered}`

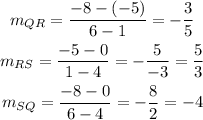
The answers are

slope of QR=-3/5, slope of RS=5/3, slope of SQ=-4

As for the length of the segments, we need to use the following formula for the distance between two points.

`d=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}`

Then,

`\begin{gathered} d_(QR)=\sqrt[]{(6-1)^2+(-8-(-5))^2}=\sqrt[]{25+9}=\sqrt[]{34} \\ d_(RS)=\sqrt[]{(1-4)^2+(-5-0)^2}\sqrt[]{9+25}=\sqrt[]{34} \\ d_(SQ)=\sqrt[]{(4-6)^2+(0-(-8))^2}=\sqrt[]{4+64}=\sqrt[]{68} \end{gathered}`

The answers are

length of QR=sqrt34, length of RS=sqrt34, length of SQ=sqrt68

Two lines (or segments) are perpendicular if their slopes satisfy the following relation

`m_1\cdot m_2=-1`

In our case, notice that

`m_(QR)\cdot m_(RS)=-(3)/(5)\cdot(5)/(3)=-1`

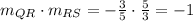
Therefore, angle

Thus, triangle QRS has a right angle and two of its sides are the same measure; hence, triangle QRS is Isosceles right.