Given:
A(1,-1), B(5,-3), C(7,1), and D(3,3)
Area of ABCD = 20.25 square units
Let's determine if the area is correct.
Since ABCD is a square, all side lengths are equal.
Now, let's find the length of one side.
Apply the distance formula:
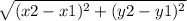
Let's find the length of AB.
Where:
(x1, y1) ==> A(1, -1)
(x2, y2) ==> B(5, -3)
Thus, we have:
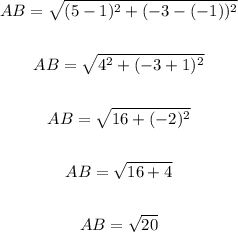
The length of one side of the square is √20.
Now, to find the area of a square, we have:

Therefore, the area of the square is 20 square units.
This means the area is not 20.25 square units.
Therefore, the