Question

Using the points A(3,7) and B(2,11) find:A: The equation of the line.

Answer 1

The given points are A(3,7) and B(2,11).

First, we find the slope of the line that passes through A and B.

`m=(y_2-y_1)/(x_2-x_1)`

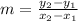
Where,

`\begin{gathered} x_1=3 \\ x_2=2 \\ y_1=7 \\ y_2=11 \end{gathered}`

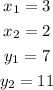
Replacing these coordinates, we have

`m=(11-7)/(2-3)=(4)/(-1)=-4`

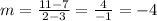
Now, we sue the slope, one point and the point-slope formula

`\begin{gathered} y-y_1=m(x-x_1) \\ y-7=-4(x-3) \\ y-7=-4x+12 \\ y=-4x+12+7 \\ y=-4x+19 \end{gathered}`

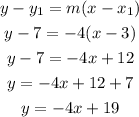
Therefore, the equation of the line is y = -4x + 19.