Question

Please see the picture below of my homework it has several parts

Answer 1

down

vertex: (0.25, 4.25)

axis of symmetry : x = 0.25

y-intercept: (0.4)

x-intercept: (-0.781, 0) and ( 1.281, 0)

Step-by-step explanation:

If we have a quadratic function of the form

`f(x)=ax^2+bx+c`

then the graph opens downward if a < 1.

The quadratic function we have is

`f(x)=-4x^2+2x+4^{}`

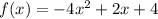
Since a = -4 < 1, the graph of the function opens downward.

The x-coordinate of the vertex of the function is given by

`x=-(b)/(2a)`

which is also the x-axis of symmetry of the graph ( the axis of symmetry passes through the vertex.

Now in our case a = -4 and b = 2; therefore, the vertex is

`x=(2)/(2\cdot4)=(2)/(8)`
`\boxed{x=0.25.}`

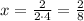
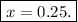
the above is the x-coordinate of the vertex. The y-coordinate is found by putting x = 0.25 into our function. This gives

`f(0.25)=-4(0.25)^2+2(0.25)+4^{}`

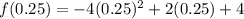
the above simplifies to give

`f(0.25)=4.25`

Hence, the coordinates of the vertex are (0.25, 4.25).

The y-intercept is found by putting x = 0 into the function. This gives

`\begin{gathered} f(0)=-4(0)^2+2(0)+4 \\ f(0)=4 \end{gathered}`

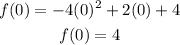
Hence, the y-intercept is at (0,4).

The x-intercepts are the soltuions to

`-4x^2+2x+4=0`

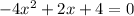
Using the quadratic formula, the solutions we get are

`x=\frac{-2\pm\sqrt[]{2^2-4(-4)(4)}}{2\cdot(-4)}`

which simplifies to give

`\begin{gathered} x=-0.781 \\ x=1.281 \end{gathered}`

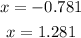
Meaning, the x-intercepts are (-0.781, 0) and ( 1.281, 0).

Hence, to summerise our answers

down

vertex: (0.25, 4.25)

axis of symmetry : x = 0.25

y-intercept: (0.4)

x-intercept: (-0.781, 0) and ( 1.281, 0)

The graph of the function is attached below.