Answer:
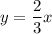
Explanation:
Hi there!
The given linear equations are organized in slope-intercept form:
 where m is the slope of the line and b is the y-intercept (the value of y when x=0)
where m is the slope of the line and b is the y-intercept (the value of y when x=0)
First, we can determine the slope using the following formula:
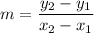 where two given points are
where two given points are
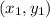 and
and
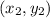
Plug in any two points from the graph that falls on the line (you can see below that I've used (3,2) and (0,0):
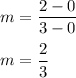
Therefore, the slope of the line is
 . Plug this into
. Plug this into
 as m:
as m:
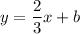
We know that the point (0,0) falls on the line. Because y=0 when x=0, we know that the y-intercept (b) is 0:
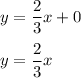
I hope this helps!