If we do not pay for the loyalty card, then our charges for p photos will be
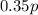
If we do pay for the loyalty card, then the cost of p photos will be
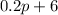
If we want the cost of the two plans the same then the above expressions must be equal; therefore, we have
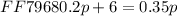
Now we solve for p by subtracting 0.2p from both sides

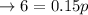

Hence, you need to print 40 photos in order to make the price of the two plans the same.