Question

find the equation of the line perpendicular to 6y=x-1 that passed through (3,5). write answer in slope intercept form, y=mx+b with all fractions written in lower terms

Answer 1

You have the following equation:

`6y=x-1`

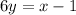
if you divide by 6 both sides, you obtain:

`y=(1)/(6)x-(1)/(6)`

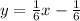
the slope of the previous line is m = 1/6.

Take into accout that the relation between the slopes of two perpendicular lines is given by:

`m^(\prime)=-(1)/(m)`

For the required perpendicular line you have:

`m^(\prime)=-(1)/((1)/(6))=-6`

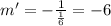
Now, use the following general equation for a line:

`y-y_o=m^(\prime)(x-x_o)`

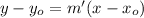
where (xo,yo) is any point on the line.

Replace (xo,yo) = (3,5) and m' = -6 into the previous formula and solve for y:

`\begin{gathered} y-5=-6(x-3) \\ y-5=-6x+18 \\ y=-6x+18+5 \\ y=-6x+23 \end{gathered}`

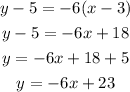
Hence, the equation of the perpendicular line is, in intercept slope form:

y = -6x + 23