Question:
Given
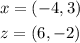
Find the coordinates of Y if Y belongs to the segment XZ and divides it one-fifth of the way from X to Z
Answer:
First of all, we need to know how long is the segment XZ. For this, and for all the exercise, we'll use the formula for the distance between two points on a 2D plane, that states:
![\begin{gathered} \text{Given} \\ a=\mleft(x_a,y_a\mright) \\ b=(x_b,y_b) \\ \text{The distance between a and b is} \\ d(a,b)=\sqrt[]{(x_a-x_b)^2+(y_a-y_b)^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xb92c8sd89r7ujgcwr5jsshf3xp0p1pklu.png)
Let's apply the formula to X and Z
![\begin{gathered} d(x,z)=\sqrt[]{(-4-6)^2+(3-(-2))^2} \\ \rightarrow d(x,z)=\sqrt[]{(-4-6)^2+(3+2)^2} \\ \rightarrow d(x,z)=\sqrt[]{(-10)^2+(5)^2} \\ \rightarrow d(x,z)=\sqrt[]{100+25} \\ \rightarrow d(x,z)=\sqrt[]{125} \\ \text{Therefore, } \\ d(x,z)=5\sqrt[]{5},\text{ aprox 11.18} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f5a21sdaw18dvm5k5sqafye8cw4tppvr78.png)
We know that the distance from X to Y is 1/5 of the distance from X to Z, and that the distance between Y an Z is 4/5. Hence Y splitting the segment "one-fifth of the way"
Therefore,
![d(x,y)=(1)/(5)* d(x,z)\text{ }\rightarrow d(x,y)=(1)/(5)*5\sqrt[]{5}\text{ }\rightarrow d(x,y)=\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/quaqxsbqgd8jrv6wzq9keg22xwdth5sx6u.png)
Meaning that
![\begin{gathered} \sqrt[]{(-4-x_y)^2+(3-y_y)^2}=\sqrt[]{5} \\ \text{Square both sides,} \\ (-4-x_y)^2+(3-y_y)^2=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r81ndhy1wjn9y9drxv2vgavyrlwj3yamxw.png)
And
![d(y,z)=(4)/(5)* d(x,z)\rightarrow d(y,z)=(4)/(5)*5\sqrt[]{5}\rightarrow d(y,z)=4\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/wqgq6k54asy499w4gmakjbrw06gqgwj75y.png)
Meaning that
![\begin{gathered} \sqrt[]{(x_y-6)^2+(y_y-(-2))^2}=4\sqrt[]{5} \\ \rightarrow\sqrt[]{(x_y-6)^2+(y_y+2)^2}=4\sqrt[]{5} \\ \text{Square both sides,} \\ \rightarrow(x_y-6)^2+(y_y+2)^2=16(5) \\ \rightarrow(x_y-6)^2+(y_y+2)^2=80 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4ec4zxz55nacu73wb8h95qfjxmdqpzdbxq.png)
Now, notice we have two simultaneous equations with two unknowns. To find the coordinates of y, we just have to solve them.
Let's say that
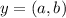
Our simultaneous equations would be
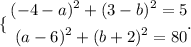
Let's expand equation 1

And equation 2
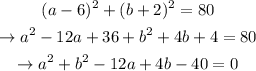
Notice equation 1 and 2 are equal to zero. We can equal equation 1 to equation 2, and get
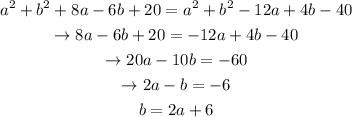
We're getting the equation of a straight line!
That means that all the points that belong to such line satisfy the distance conditions we've set from the start (dividing XZ one-fifth of the way from X to Z).
Let's call that line Line 1
Luckly, we know that our y belongs to the straight line that contains X and Z, because we're told that it belongs to XZ. We just have to find its equation and solve it simultaneously with the equation of the line we already have.

Let's call that line Line 2
We've defined that y=(a,b) , so Line 2 in those terms would be
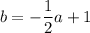
Our new, and last, set of simultanoeus equations would be

Let's equal equation 1 and 2, and solve:
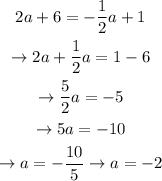
And plug in that value in any equation to find b. I'll use equation 1

And there we have the coordinates of y. Thus,
