Question

Consider the parabola given by the equation: f(x) = 4x212.0 + 6Find the following for this parabola:A) The vertex:B) The vertical intercept is the pointC) Find the coordinates of the two x-intercepts of the parabola and write them as a list, separated bycommas:It is OK to round your value(s) to to two decimal places.

Answer 1

(a)(1.5, -3)

(b)(0,6)

(c)(2.37, 0), (0.63, 0)

Step-by-step explanation:

Given the equation of the parabola:

`f\mleft(x\mright)=4x^2-12x+6`

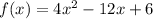
Part A

To find the vertex, first, determine the equation of the line of symmetry:

`\begin{gathered} x=-(b)/(2a) \\ =-(-12)/(2*4)=(12)/(8) \\ x=1.5 \end{gathered}`

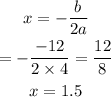
Substitute x=1.5 to find f(1.5).

`f(1.5)=4(1.5)^2-12(1.5)+6=-3`

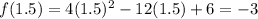
The vertex of the parabola: (1.5, -3)

Part B

The vertical intercept is the point where x=0

`\begin{gathered} f\mleft(0\mright)=4(0)^2-12(0)+6 \\ f(0)=6 \end{gathered}`

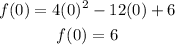
The vertical intercept is the point (0,6).

Part C

The x-intercepts are the point where f(x)=0.

`f\mleft(x\mright)=4x^2-12x+6=0`

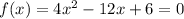
From the equation above: a=4, b=-12, c=6

Using the quadratic formula:

`\begin{gathered} x=(-b\pm√(b^2-4ac) )/(2a) \\ =\frac{-(-12)\pm\sqrt[]{(-12)^2-4(4)(6)}}{2*4} \\ =\frac{12\pm\sqrt[]{144-96}}{8} \\ =\frac{12\pm\sqrt[]{48}}{8} \end{gathered}`

Therefore:

`\begin{gathered} x=\frac{12+\sqrt[]{48}}{8}\text{ or }x=\frac{12-\sqrt[]{48}}{8} \\ x=2.37\text{ or }x=0.63 \end{gathered}`

The coordinates of the two x-intercepts of the parabola are:

• (2.37, 0)

,

• (0.63, 0)