Question

What volume will 12 g of oxygen gas (O2) occupy at 25 °C and a pressure of 53 kPa?

Answer 1

The volume of the oxygen gas is 17.5 L

Step-by-step explanation

Given that;

The mass of oxygen gas is 12 grams

The temperature of the gas is 25 degrees Celcius

The pressure of the gas is 53 kPa

To find the volume of the oxygen gas, follow the steps below

Step 1; Assume the gas behaves like an ideal gas

Therefore, apply the ideal gas equation to find the volume of the gas

`\text{ PV }=\text{ nRT}`

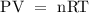
Where

P is the pressure of the gas

V is the volume of the gas

n is number of moles of the gas

R is the universal gas constant

T is the temperature of the gas

Step 2: Find the number of moles of the oxygen gas using the below formula

`\text{ mole }=\text{ }\frac{\text{ mass}}{\text{ molar mass}}`

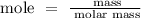
Recall, that the molar mass of the oxygen gas is 32 g/mol

`\begin{gathered} \text{ mole }=\text{ }\frac{12}{\text{ 32}} \\ \text{ mole }=\text{ 0.375 mol} \end{gathered}`

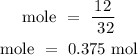
Step 3; Convert the temperature to degree Kelvin

`\begin{gathered} \text{ T }=\text{ t }+\text{ 273.15} \\ \text{ t }=\text{ 25}\degree C \\ \text{ T }=25\text{ }+\text{ 273.15} \\ \text{ T }=\text{ 298.15K} \end{gathered}`

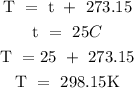
Step 4; Substitute the given data into the formula in step 1

Recall, that R is 8.314 L kPa K^-1 mol^-1

`\begin{gathered} \text{ 53 }*\text{ V }=\text{ 0.375}*\text{ 8.314}*\text{ 298.15} \\ \text{ 53V }=\text{ 929.557} \\ \text{ Divide both sides by 53} \\ \text{ }\frac{\cancel{53}V}{\cancel{53}}\text{ }=\text{ }(929.557)/(53) \\ \text{ V }=\text{ }(929.557)/(93) \\ \text{ V }=\text{ 17.5 L} \end{gathered}`

Hence, the volume of the oxygen gas is 17.5 L