Answer:
(-8,0)
Step-by-step explanation:
If we have an equation with the form:
y = ax² + bx + c
The x-coordinate of the vertex will be: -b/2a
So, in this case, for the equation:
y = x² + 16x + 64
Where a = 1, b = 16, and c = 64
We get that the x-coordinate of the vertex is:
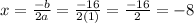
Then, the y-coordinate can be calculated replacing x by -8 on the initial equation, so:
y = (-8)² + 16(-8) + 64
y = 64 - 128 +64
y = 0
Therefore, the vertex of the parabola is the point (-8, 0)