Question

You need 520 mL of a 40% alcohol solution. On hand, you have a 65% alcohol mixture. How much of the 65%alcohol mixture and pure water will you need to obtain the desired solution?You will needmL of pure waterandmL of the 65% solution.Question Help: Message instructorSubmit Question

Answer 1

We have to find how much 65% alcohol mixture it is needed to prepare a 520 mL of a 40% alcohol solution.

We can write two equations: one for the volume and one for the concentration.

Let A be the volume of alcohol of 65% concentration and W the volume of water.

Then, for the volume, we can write:

`A+W=520`

as the sum of the alcohol mixture and the water is equal to the final volume of 520 mL.

For the concentration, we can write:

`\begin{gathered} 0.65\cdot A+0\cdot W=0.40\cdot520 \\ 0.65A=208 \end{gathered}`

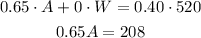
In this case we multiply the concentration by the volume of each component and this is equal to the final concentration multiplied by the final volume.

As we just want to find A, we can use this last equation to calculate it.

`\begin{gathered} 0.65A=208 \\ A=(208)/(0.65) \\ A=320 \end{gathered}`

Then, to have a 520 mL volume of 40% concentration alcohol we need 320 mL of 65% alcohol mixture and the rest of the volume in water.

The volume of water is:

`\begin{gathered} A+W=520 \\ W=520-A=520-320=200 \end{gathered}`

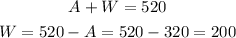
Answer:

You will need 200 mL of pure water and 320 mL of the 65% solution.