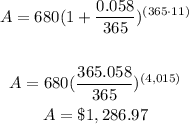Question

Matthew invested $680 in an account paying an interest rate of 5.8% compoundeddaily. Assuming no deposits or withdrawals are made, how much money, to thenearest ten dollars, would be in the account after 11 years?

Answer 1

Matthew invested $680 in an account paying an interest rate of 5.8% compounded

daily. Assuming no deposits or withdrawals are made, how much money, to the

nearest ten dollars, would be in the account after 11 years?

we know that

The compound interest formula is equal to

`A=P(1+(r)/(n))^(nt)`

`A=P(1+(r)/(n))^(nt)`

where

A is the Final Investment Value

P is the Principal amount of money to be invested

r is the rate of interest in decimal

t is Number of Time Periods

n is the number of times interest is compounded per year

in this problem we have

P=$680

r=5.8%=5.8/100=0.058

n=365

t=11 years

substitute in the formula

`\begin{gathered} A=680(1+(0.058)/(365))^((365\cdot11)) \\ \\ A=680((365.058)/(365))^((4,015)) \\ A=\$1,286.97 \end{gathered}`