For the situational card, Blake needs one and he has 5, so there are 5 possible choices.
For the power card, he needs 1 from 4, so there are 4 possible choices.
For the level card, he needs 1 from 10, so there are 10 possible choices.
The number of different complete sets will be the product of the possible choices of each card:
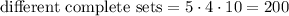
So there are 200 different complete sets that can be made.