Question

A baseball pitcher won 85 % of the games he pitched. If he pitched 40 ballgames , how many games did he win ?

Answer 1

The total games pitched is 40

Let number of games he win be y.

Then the ratio of the game win to the total game is

`(y)/(40)`

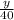
The percentage of game won by the pitcher is

`85\text{ \%}`

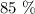
Then, the ratio of this percentage will be

`(85)/(100)`

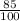
Equate both ratio we have

`(y)/(40)=(85)/(100)`

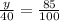
Take cross product of the equation above

`\begin{gathered} 100y=85*40 \\ 100y=3400 \end{gathered}`

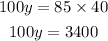
Divide both sides of the equation by 100.

`\begin{gathered} (100y)/(100)=(3400)/(100) \\ \text{Then} \\ y=34 \end{gathered}`

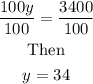
Therefore, the Baseball picher won 34 of the games he pitched.

Answer is 34