You have the following equation:
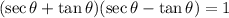
In order to demostrate that the left side of the equation is equal to the right side, you first use the fact that the product between the factors in the left side are the factor of a squares difference, that is:
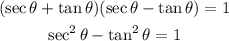
Furthermore, sec²θ = 1/cos²θ and tan²θ = sin²θ/cos²θ, then, by using these expressions you obtain:
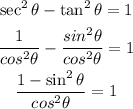
Furthermore, you have that cos²θ + sin²θ = 1, hence, 1 - sin²θ = cos²θ. You replace this expression and obtain:
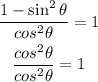
The last result is the demonstration of the idenity