ANSWER
10.0 m/s
Step-by-step explanation
The ore cart has a mass m1 of 1200kg, and rolls at a speed v1 of 12.8 m/s. Then a crane dumps 338 kg of extra ore into the cart, so now the mass is m2 = m1 + 338 kg = 1538 kg. We want to find the new speed v2 of the ore cart.
By law of conservation of momentum we have:
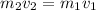
Solving for v2:
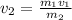
And replacing with the values:
![v_2=\frac{1200\operatorname{kg}\cdot12.8m/s}{1538\operatorname{kg}}=10.0m/s]()
The speed of the ore cart is now 10.0 m/s, rounded to the nearest tenth