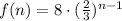A geometric sequence is a sequence of numbers where consecutive elements have a common ratio r:
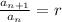
Then, we can find the next element of the sequence by multiplying the preceding element by the common ratio r:
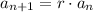
If the first element of the sequence is a₁, then:
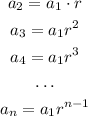
The given information states that a₁=8 and that the common ratio is 2/3.
Then, substitute a₁=8 and r=2/3 into the expression for the n-th term:
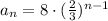
Therefore, the sequence can be written as a function as follows: